Next: About this document ... Up: Aplikace lineární algebry Previous: Kreslíme krychli
Tato kapitola si klade za úkol, ukázat, že přepočítávání souřadnic z jedné báze do
druhé může být celkem užitečná věc. V podstatě si ukážeme, jak funguje kompresní algoritmus,
který používá velmi známý formát na ukládání obrázků jpg. Začneme s poněkud umělým ale názorným
příkladem, z kterého bude patrné, o co nám půjde. Představme si, že máme za úkol zkomprimovat
signály s dvěma vzorky, tj. naše signály mají tento tvar
![]() . Může jít například
o jakási dvě měření, která proběhla za sebou a jejich výsledkem byly hodnoty
. Může jít například
o jakási dvě měření, která proběhla za sebou a jejich výsledkem byly hodnoty ![]() a
a ![]() .
Dále předpokládejme, že naše měření
.
Dále předpokládejme, že naše měření ![]() jsou celá čísla z intervalu
jsou celá čísla z intervalu
![]() , tj.
náš signál obsahuje dva byty. Naším úkolem je aproximovat vektory
, tj.
náš signál obsahuje dva byty. Naším úkolem je aproximovat vektory
![]() pomocí jen jednoho celého čísla
pomocí jen jednoho celého čísla ![]() z intervalu
z intervalu
![]() , tak abychom byli schopni z čísla
, tak abychom byli schopni z čísla ![]() zpětně zrekonstruovat
původní vektor
zpětně zrekonstruovat
původní vektor ![]() , pokud možno s co největší přesností. Tím vlastně dojde k oné kompresi.
Spojením ``s co největší přesností'' máme na mysli to, aby vzdálenost mezi koncovými body vektoru
, pokud možno s co největší přesností. Tím vlastně dojde k oné kompresi.
Spojením ``s co největší přesností'' máme na mysli to, aby vzdálenost mezi koncovými body vektoru
![]() a zrekonstruovaného vektoru
a zrekonstruovaného vektoru ![]() byla pokud možno co nejmenší, tj. chceme aby
byla pokud možno co nejmenší, tj. chceme aby
![]() bylo malé.
Nakonec budeme předpokládat, že naše měření
bylo malé.
Nakonec budeme předpokládat, že naše měření ![]() jsou vždy přibližně stejné hodnoty.
jsou vždy přibližně stejné hodnoty.
Jedna z možností jak tuto úlohu řešit, je reprezentovat každý vektor ![]() pomocí souřadnic v nějaké vhodně
zvolené uspořádané bázi
pomocí souřadnic v nějaké vhodně
zvolené uspořádané bázi
![]() a následně vektor
a následně vektor ![]() popsat jen pomocí první souřadnice
v této bázi. Přesněji řečeno, pokud
popsat jen pomocí první souřadnice
v této bázi. Přesněji řečeno, pokud
![]() , pak ono hledané číslo je
, pak ono hledané číslo je ![]() a zrekonstruovaný
vektor
a zrekonstruovaný
vektor
![]() . Samozřejmě číslo
. Samozřejmě číslo ![]() je obecně reálné číslo, takže je potřeba ho ještě
zaokrouhlit a báze
je obecně reálné číslo, takže je potřeba ho ještě
zaokrouhlit a báze ![]() musí být zvolena tak, aby padlo do intervalu
musí být zvolena tak, aby padlo do intervalu
![]() . To je, ale technická
záležitost, která není pro vysvětlení užití lineární algebry v kompresi důležitá.
. To je, ale technická
záležitost, která není pro vysvětlení užití lineární algebry v kompresi důležitá.
Otázkou tedy je, jakou uspořádanou bázi pro tento účel použít.
Pokud bychom vzali za ![]() přímo standardní bázi
přímo standardní bázi ![]() , pak bychom popisovali vektor
, pak bychom popisovali vektor
![]() číslem
číslem ![]() . Tato volba by ale byla dobrá, jen v případě, že bychom předpokládali, že druhé měření
. Tato volba by ale byla dobrá, jen v případě, že bychom předpokládali, že druhé měření ![]() je
blízké nule. Vzdálenost
je
blízké nule. Vzdálenost
![]() je totiž v tomto případě rovna
je totiž v tomto případě rovna ![]() .
My ale předpokládáme, že hodnoty
.
My ale předpokládáme, že hodnoty ![]() jsou přibližně stejné. Proto bude lepší vzít za
jsou přibližně stejné. Proto bude lepší vzít za ![]() tuto bázi
tuto bázi
![]() . Spočtěte si, že v tomto případě souřadnice vektoru
. Spočtěte si, že v tomto případě souřadnice vektoru ![]() vzhledem k bázi
vzhledem k bázi ![]() jsou
jsou
![]() .
Vektor
.
Vektor ![]() budeme tedy v tomto případě aproximovat pomocí aritmetického průměru
budeme tedy v tomto případě aproximovat pomocí aritmetického průměru ![]() , což je celkem
přirozená volba vzhledem k našemu předpokladu blízkosti čísel
, což je celkem
přirozená volba vzhledem k našemu předpokladu blízkosti čísel ![]() a
a ![]() . Zrekonstruovaný vektor tedy je
. Zrekonstruovaný vektor tedy je
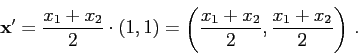
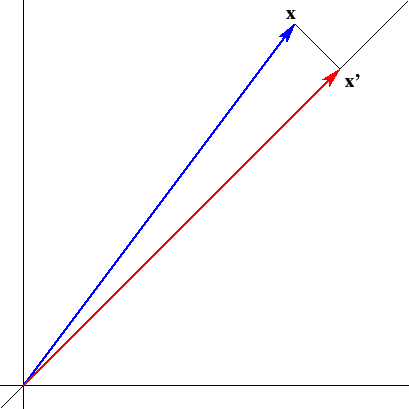
Originální modrý vektor ![]() leží poblíž přímky procházející počátkem se směrovým vektorem
leží poblíž přímky procházející počátkem se směrovým vektorem ![]() , protože předpokládáme,
že hodnoty
, protože předpokládáme,
že hodnoty ![]() jsou přibližně stejné. My tento vektor aproximujeme ortogonální projekcí, což je ten červený vektor
jsou přibližně stejné. My tento vektor aproximujeme ortogonální projekcí, což je ten červený vektor ![]() .
.
Dříve než přistoupíme k samotné kompresi obrázků, zobecněme náš příklad se signály tvaru ![]() do vyšší dimenze.
Tentokrát budeme mít signály s osmi vzorky, tj. signály tvaru
do vyšší dimenze.
Tentokrát budeme mít signály s osmi vzorky, tj. signály tvaru
![]() . Opět budeme předpokládat,
že hodnoty
. Opět budeme předpokládat,
že hodnoty ![]() se nemění příliš rychle, tj. rozdíly mezi sousedními vzorky
se nemění příliš rychle, tj. rozdíly mezi sousedními vzorky ![]() ,
, ![]() , jsou malé.
Postup bude stejný. Zvolíme nějakou vhodnou uspořádanou bázi
, jsou malé.
Postup bude stejný. Zvolíme nějakou vhodnou uspořádanou bázi
![]() a vyjádříme vektor
a vyjádříme vektor ![]() v této bázi, tj. najdeme jeho souřadnice v bázi
v této bázi, tj. najdeme jeho souřadnice v bázi ![]() . Následně zahodíme ty souřadnice, jejichž hodnoty budou velmi malé
(v porovnání s ostatními). Tím budeme aproximovat vektor
. Následně zahodíme ty souřadnice, jejichž hodnoty budou velmi malé
(v porovnání s ostatními). Tím budeme aproximovat vektor ![]() z prostoru dimenze osm vektorem
z prostoru dimenze osm vektorem ![]() z prostoru s menší dimenzí.
z prostoru s menší dimenzí.
Způsob jak vybrat vhodnou bázi ![]() není úplně jednoduchý. Existuje mnoho možností a každá má své výhody a nevýhody.
My zde použijeme bázi, která se používá v diskrétní kosinové transformaci (viz tyto stránky).
Porovnejte zde uvedený postup také s teorií, kterou se budete učit v předmětu Matematika 2
v části o Fourierových řadách.
není úplně jednoduchý. Existuje mnoho možností a každá má své výhody a nevýhody.
My zde použijeme bázi, která se používá v diskrétní kosinové transformaci (viz tyto stránky).
Porovnejte zde uvedený postup také s teorií, kterou se budete učit v předmětu Matematika 2
v části o Fourierových řadách.
Definujme tedy naši bázi
![]() . Pro
. Pro ![]() , označme
, označme ![]() -tou složku vektoru
-tou složku vektoru ![]() symbolem
symbolem ![]() , tj.
, tj.
![]() . Pak
. Pak
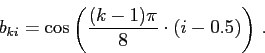
![\includegraphics[width=20cm,height=10cm]{baze}](img112.png)
Tyto stránky si nekladou za cíl přesně vysvětlit, proč je tato volba dobrá. Spokojme se s neformálním vysvětlením. Protože předpokládáme,
že změny v našem signálu ![]() nejsou velké, je dobré mít v bázi
nejsou velké, je dobré mít v bázi ![]() vektory, jejichž sousední hodnoty se mění jen o málo a naopak také vektory
jejichž sousední hodnoty se mění hodně. Konkrétně v naší bázi
vektory, jejichž sousední hodnoty se mění jen o málo a naopak také vektory
jejichž sousední hodnoty se mění hodně. Konkrétně v naší bázi ![]() vektory na začátku (tj.
vektory na začátku (tj.
![]() ) jsou vektory, jejichž
sousední hodnoty se mění pozvolna. Naopak sousední hodnoty vektorů na konci (tj.
) jsou vektory, jejichž
sousední hodnoty se mění pozvolna. Naopak sousední hodnoty vektorů na konci (tj.
![]() ) se mění výrazněji.
Pokud najdeme souřadnice našeho málo měnícího se signálu
) se mění výrazněji.
Pokud najdeme souřadnice našeho málo měnícího se signálu ![]() v této bázi, budou souřadnice odpovídající bázovým vektorům
v této bázi, budou souřadnice odpovídající bázovým vektorům
![]() velké v porovnání se souřadnicemi, které odpovídají bázovým vektorům
velké v porovnání se souřadnicemi, které odpovídají bázovým vektorům
![]() . Ukažme si to na příkladě.
Vezměme následující skript pro program Octave:
. Ukažme si to na příkladě.
Vezměme následující skript pro program Octave:
t=(1:8)'; % indexy vzorku B=zeros(8,8); % B bude matice prechodu od standardni baze k nami zvolene bazi (B) % Spocti bazove vektory b_k a napln jimi sploupce matice B for k=1:8 B(:,k)=cos(pi*(k-1)*(t-0.5)/8); endfor x=3+0.1*(t-4).^2+0.5*rand(8,1); % vyrob nejaky malo se menici signal y=inv(B)*x; % y jsou souradnice x v bazi (B) yap=y; yap(5:8)=0; % do yap dej y a posledni 4 souradnice vynuluj xap=B*yap; % spocti aproximaci puvodniho vektoru figure(1); bar([x,xap]); % vykresli puvodni signal a jeho aproximaci figure(2); bar(y); % vykresli souradnice x v (B)Tento skript vyrobí málo se měnící signál
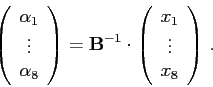
Konkrétní ukázky, které vypadly ze skriptu jsou tyto:
![\includegraphics[width=20cm,height=10cm]{aprox2}](img124.png)
Vlevo vidíme původní signál ![]() (modrá barva) a jeho aproximaci
(modrá barva) a jeho aproximaci ![]() (červená barva). Vpravo vidíme souřadnice vektoru
(červená barva). Vpravo vidíme souřadnice vektoru ![]() v bázi
v bázi ![]() .
Všimněte si, že souřadnice odpovídající vektorům
.
Všimněte si, že souřadnice odpovídající vektorům
![]() jsou mnohem větší než zbývající souřadnice. To je dáno tím, že se sousední
hodnoty našeho signálu
jsou mnohem větší než zbývající souřadnice. To je dáno tím, že se sousední
hodnoty našeho signálu ![]() nemění příliš rychle.
nemění příliš rychle.
A toto je v podstatě princip, na kterém je založen algoritmus pro ukládání fotek ve formátu jpg. Obecně totiž předpokládáme, že fotky v sobě neobsahují příliš
mnoho rychle měnících se oblastí. Naopak velmi často obsahují oblasti, kde se jas mění jen nepatrně. Postup si ukážeme na černobílé fotce. S barevnými
fotkami se dělá to samé třikrát pro každou barevnou složku zvlášť. Fotku si můžeme představit jako matici, jejíž jednotlivé hodnoty představují hodnoty
jasu jednotlivých pixelů. Např. matice typu ![]()
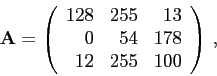

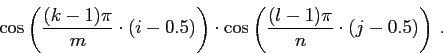
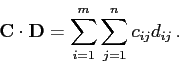
Ukažme si několik bázových vektorů
![]() . Protože dole bude následovat příklad s maticí typu
. Protože dole bude následovat příklad s maticí typu ![]() , ukážeme si
bázové vektory tohoto typu. Matice
, ukážeme si
bázové vektory tohoto typu. Matice
![]() je podobně jako v předchozím příkladě konstantní, tj. všechny její prvky jsou stejné
a rovné
je podobně jako v předchozím příkladě konstantní, tj. všechny její prvky jsou stejné
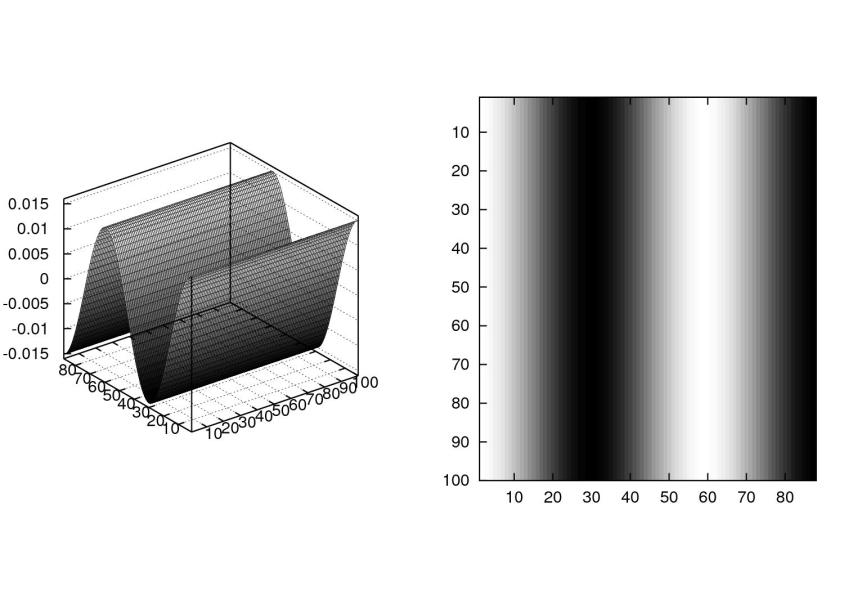
a rovné ![]() . Pokud vezmeme první index větší než jedna, začne se projevovat kosinus ve svislém směru. Např.
. Pokud vezmeme první index větší než jedna, začne se projevovat kosinus ve svislém směru. Např.
![]() vypadá takto:
vypadá takto:
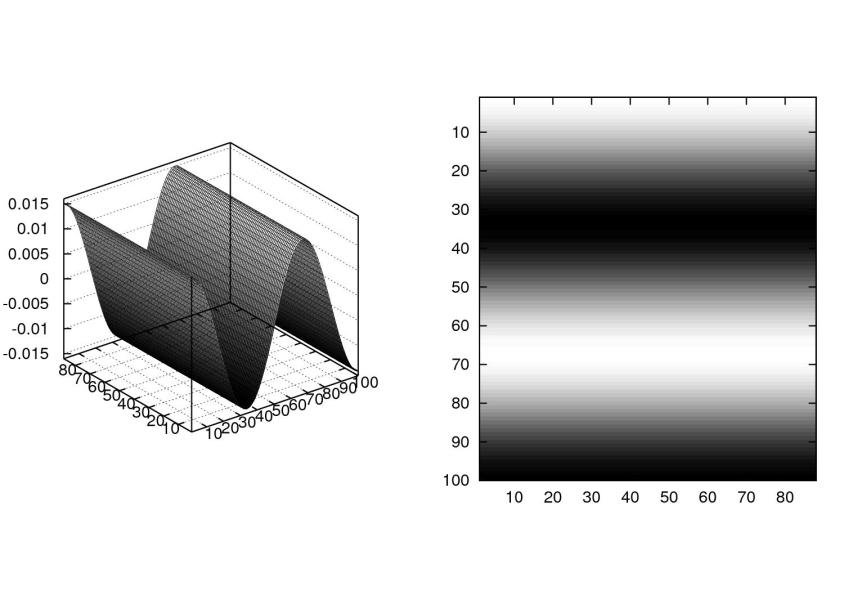
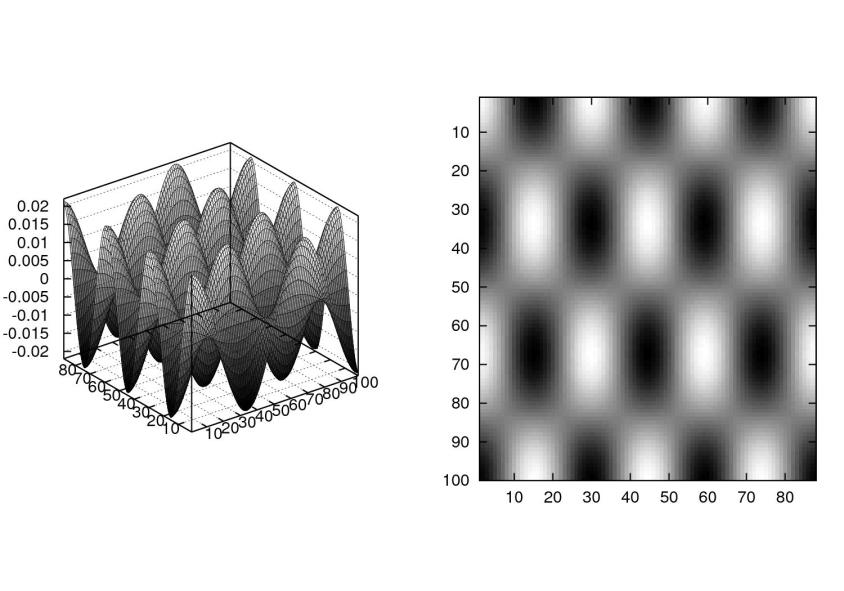
Podobně pokud vezmeme druhý index větší než jedna, začne se projevovat kosinus ve vodorovném směru. Např.
![]() vypadá takto:
vypadá takto:
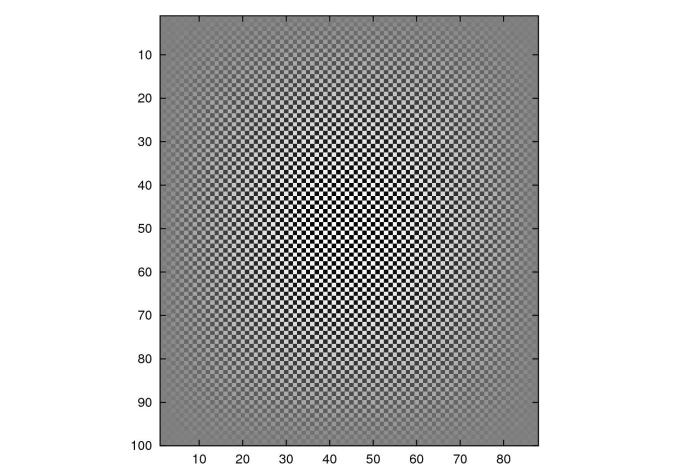
Zvětšováním obou indexů se bude frekvence obou kosinů dále zvětšovat, tj. matice
![]() má u obou kosinů nejkratší periody a vypadá takto:
má u obou kosinů nejkratší periody a vypadá takto:
Nyní si ukážeme konkrétní příklad fotky s rozměry 100x88, kterou vyjádříme ve výše uvedené bázi
![]() .
Skutečný algoritmus, který je použit ve formátu jpg rozdělí každou fotku na malé čtverečky o rozměrech 8x8 a na nich nezávisle aplikuje přepočet souřadnic.
My to tady uděláme s celou fotkou najednou. Je to sice výpočetně náročné, ale alespoň budeme moci lépe porovnat originální fotku s její aproximací.
Na čtvercích velikosti 8x8 toho totiž není mnoho patrného. Přesný popis formátu jpg a v něm použitého kompresního algoritmu najdete
zde.
.
Skutečný algoritmus, který je použit ve formátu jpg rozdělí každou fotku na malé čtverečky o rozměrech 8x8 a na nich nezávisle aplikuje přepočet souřadnic.
My to tady uděláme s celou fotkou najednou. Je to sice výpočetně náročné, ale alespoň budeme moci lépe porovnat originální fotku s její aproximací.
Na čtvercích velikosti 8x8 toho totiž není mnoho patrného. Přesný popis formátu jpg a v něm použitého kompresního algoritmu najdete
zde.
Vezměme následující fotku zpěvačky Britney Spears.

Proč zrovna tato zpěvačka. Nevím přesně, asi mi přišlo komické říkat, že vezmeme Britney Spears a vyjádříme jí v jiné bázi. Každopádně tím, že nám její fotka poslouží k vysvětlení problematiky formátu jpg, se její život jistě stane záslužnější. Původně tato fotka má rozměry 100x88, ale tady jsem ji zobrazil trochu zvětšenou.
Označme matici odpovídající této fotce ![]() . Tj.
. Tj. ![]() je matice typu
je matice typu ![]() a její složky jsou celá čísla z intervalu
a její složky jsou celá čísla z intervalu
![]() představující hodnoty jasu jednotlivých pixelů.
Podobně jako výše najdeme souřadnice
představující hodnoty jasu jednotlivých pixelů.
Podobně jako výše najdeme souřadnice ![]() v bázi
v bázi ![]() , potom některé souřadnice vynulujeme, čímž získáme
aproximaci původního obrázku vektorem z prostoru menší dimenze. To je náplní následujícího skriptu pro program Octave
(k tomu aby Vám fungoval je potřeba mít nainstalován image toolbox):
, potom některé souřadnice vynulujeme, čímž získáme
aproximaci původního obrázku vektorem z prostoru menší dimenze. To je náplní následujícího skriptu pro program Octave
(k tomu aby Vám fungoval je potřeba mít nainstalován image toolbox):
I=imread("britney2.jpg"); % nacte obrazek
I=I(:,:,1); % protoze je obrazek cernobily obsahuje 3 stejne barevne slozky RGB
% vezmi jednu z nich a dej ji do matice I
figure(1);
imshow(I); % zobraz originalni obrazek
axis equal;
I=cast(I,"double")-128; % pretypuj hodnoty jasu na realna cisla a posun do rozsahu <-128,127>
[m,n]=size(I); % zjisti velikost obrazku
[j,i]=meshgrid(1:n,1:m); % priprav definicni obor pro bazove matice Bkl
for l=1:n
for k=1:m
Bkl=cos(pi*(k-1)*(i-0.5)/m).*cos(pi*(l-1)*(j-0.5)/n); % spocti bazovou matici Bkl
v=sqrt(Bkl(:)'*Bkl(:)); % spocti jeji velikost
Bkl(:)=Bkl(:)/v; % udelej z Bkl vektor velikosti 1
S=Bkl.*I;
J(k,l)=sum(S(:)); % spocti souradnici odpovidajici Bkl pomoci skalarniho soucinu
endfor
endfor % nyni matice J obsahuje souradnice I v bazi (B)
J=round(J/16); % vydel vsechny souradnice 16 aby byly v rozsahu <-128,127> a udelej z nich cela cisla
figure(2);
surf(J); axis equal; % nakresli 3D graf se souradnicemi J
J25=J; J75=J; % promenne pro souradnice aproximaci
J25(round(m/2):end,:)=0; % J25 je matice J, kde se vynuluje 75% souradnic
J25(:,round(n/2):end)=0;
J75(round(m/2):end,round(n/2):end)=0; % J75 je matice J, kde se vynulule 25% souradnic
RI25=zeros(m,n); RI75=zeros(m,n); % promenne pro vlastni aproximace
for l=1:n
for k=1:m
Bkl=cos(pi*(k-1)*(i-0.5)/m).*cos(pi*(l-1)*(j-0.5)/n); % spocti bazovou matici Bkl
v=sqrt(Bkl(:)'*Bkl(:));
Bkl(:)=Bkl(:)/v; % udelej z ni vektor velikosti 1
A=16*J25(k,l)*Bkl; % spocitej prispek matice Bkl podle souradnic z J25. Nasobime 16, protoze jsme predtim veschny souradnice 16 vydelili.
RI25=RI25+A; % pricti tento prispevek k R25
A=16*J75(k,l)*Bkl; % spocitej prispek matice Bkl podle souradnic z J75. Nasobime 16, protoze jsme predtim veschny souradnice 16 vydelili.
RI75=RI75+A; % pricti tento prispevek k R25
endfor
endfor % matice R25 tedy rovna linearni kombinaci bazovych matic Bkl s koeficienty J25
% matice R75 tedy rovna linearni kombinaci bazovych matic Bkl s koeficienty J75
figure(3);
imshow(uint8(RI75+128)); % zobraz aproximaci po vymazani 25% dat
axis equal;
figure(4);
imshow(uint8(RI25+128)); % zobraz aproximaci po vymazani 75% dat
axis equal;
Vysvětleme si, co tento skript dělá. Poté co zobrazí originální obrázek, odečte od všech hodnot v matici ![]() číslo
číslo ![]() .
Tím se její hodnoty dostanou do rozsahu
.
Tím se její hodnoty dostanou do rozsahu
![]() . To se dělá pravděpodobně kvůli tomu, aby souřadnice odpovídající
bázové matici
. To se dělá pravděpodobně kvůli tomu, aby souřadnice odpovídající
bázové matici
![]() nebyla příliš velká v porovnání s ostatními souřadnicemi. Dále tento skript přepočítá souřadnice matice
nebyla příliš velká v porovnání s ostatními souřadnicemi. Dále tento skript přepočítá souřadnice matice
![]() do báze
do báze ![]() . Protože je báze
. Protože je báze ![]() ortonormální, je to jednoduché. Jak víme z přednášky, souřadnice vůči ortonormální
bázi, lze vyjádřit jako skalární součiny matice
ortonormální, je to jednoduché. Jak víme z přednášky, souřadnice vůči ortonormální
bázi, lze vyjádřit jako skalární součiny matice ![]() s jednotlivými bázovými maticemi
s jednotlivými bázovými maticemi
![]() .
Tím dostaneme
.
Tím dostaneme ![]() souřadnic matice
souřadnic matice ![]() v bázi
v bázi ![]() , které skript uloží do matice
, které skript uloží do matice ![]() . Jednotlivé hodnoty
v matici
. Jednotlivé hodnoty
v matici ![]() , ale nemusí být v rozsahu
, ale nemusí být v rozsahu
![]() (tj. na jejich uložení bychom potřebovali více než 1 byte).
Proto všechny hodnoty v matici
(tj. na jejich uložení bychom potřebovali více než 1 byte).
Proto všechny hodnoty v matici ![]() vydělíme
vydělíme ![]() , abychom je dostali opět do rozsahu
, abychom je dostali opět do rozsahu
![]() , a zaokrouhlíme.
3D graf hodnot v matici
, a zaokrouhlíme.
3D graf hodnot v matici ![]() po tomto přeškálování vypadá takto:
po tomto přeškálování vypadá takto:
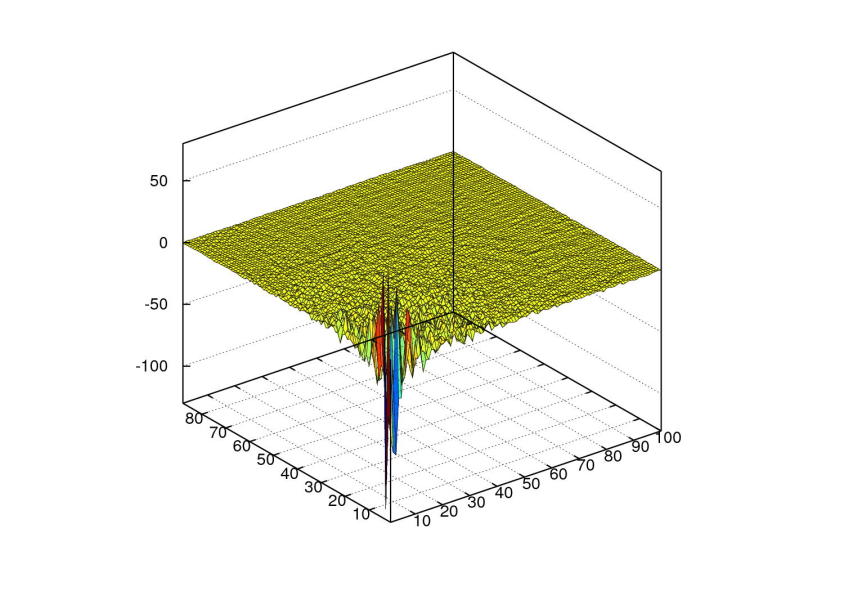
Vidíme, že velké hodnoty mají jenom souřadnice, které odpovídají bázovým maticím
![]() s malými indexy
s malými indexy ![]() a
a ![]() .
Takže opět jako předtím, můžeme nějaké malé souřadnice zanedbat (což znamená vynulovat je) a aproximovat původní obrázek
jeho ortogonální projekcí do lin. podprostoru generovaného nějakou podmnožinou báze
.
Takže opět jako předtím, můžeme nějaké malé souřadnice zanedbat (což znamená vynulovat je) a aproximovat původní obrázek
jeho ortogonální projekcí do lin. podprostoru generovaného nějakou podmnožinou báze ![]() . V našem případě spočteme dvě aproximace.
První kde zanedbáme 25% původních souřadnic a druhou kde zanedbáme 75%. Skript vyrobí dvě matice
. V našem případě spočteme dvě aproximace.
První kde zanedbáme 25% původních souřadnic a druhou kde zanedbáme 75%. Skript vyrobí dvě matice
![]() a
a
![]() .
Matice
.
Matice
![]() vznikne z matice
vznikne z matice ![]() vynulováním souřadnic, které odpovídají bázovým maticím
vynulováním souřadnic, které odpovídají bázovým maticím
![]() s indexy většími než
s indexy většími než ![]() a
a ![]() , tj.
, tj. ![]() a
a ![]() . 3D graf hodnot matice
. 3D graf hodnot matice
![]() vypadá takto:
vypadá takto:
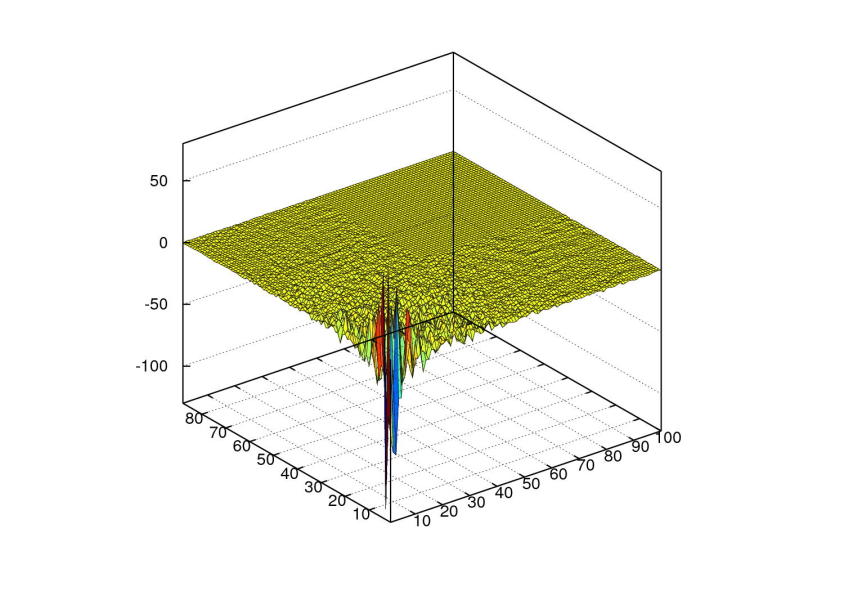
Matice
![]() vznikne z matice
vznikne z matice ![]() vynulováním souřadnic, které odpovídají bázovým maticím
vynulováním souřadnic, které odpovídají bázovým maticím
![]() s indexy kde
s indexy kde ![]() nebo
nebo ![]() . 3D graf hodnot matice
. 3D graf hodnot matice
![]() vypadá takto:
vypadá takto:
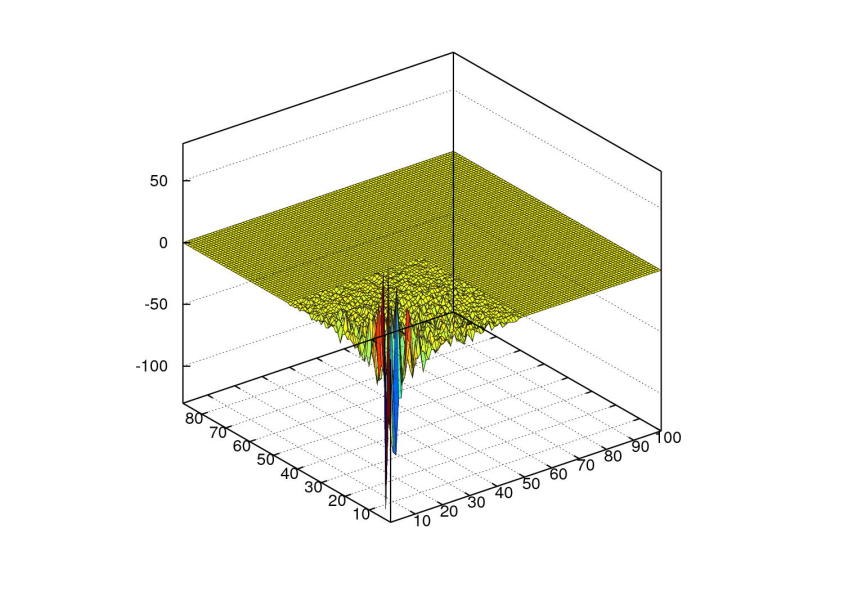
Matice
![]() a
a
![]() představují onu kompresi. Na jejich uložení totiž nepotřebujeme 8800 bytů, ale
jen 6600 v případě matice
představují onu kompresi. Na jejich uložení totiž nepotřebujeme 8800 bytů, ale
jen 6600 v případě matice
![]() a 2200 v případě matice
a 2200 v případě matice
![]() . Poznamenejme, že skutečný algoritmus
používaný ve formátu jpg je trochu složitější a nedělá jen ortogonální projekci, jako jsme udělali my. Skutečný algoritmus používá tzv. kvantizační matici, která
vyjadřuje jak je lidské oko citlivé na vnímání jednotlivých frekvencí v obrazu. Touto maticí ováží jednotlivé souřadnice v matici
. Poznamenejme, že skutečný algoritmus
používaný ve formátu jpg je trochu složitější a nedělá jen ortogonální projekci, jako jsme udělali my. Skutečný algoritmus používá tzv. kvantizační matici, která
vyjadřuje jak je lidské oko citlivé na vnímání jednotlivých frekvencí v obrazu. Touto maticí ováží jednotlivé souřadnice v matici
![]() . Po zaokrouhlení mu poté zbude jen málo nenulových souřadnic (detaily viz tyto stránky).
. Po zaokrouhlení mu poté zbude jen málo nenulových souřadnic (detaily viz tyto stránky).
Na konec výše uvedený skript zpětně zrekonstruuje z matic
![]() a
a
![]() původní obraz
původní obraz ![]() .
Tím, že jsme ale některé souřadnice vynulovali, nedostaneme původní obraz, ale jen jeho aproximace.
Vezmeme tedy souřadnice z matic
.
Tím, že jsme ale některé souřadnice vynulovali, nedostaneme původní obraz, ale jen jeho aproximace.
Vezmeme tedy souřadnice z matic
![]() a
a
![]() , vynásobíme je
, vynásobíme je ![]() (protože jsme je předtím
(protože jsme je předtím ![]() dělili)
a spočítáme lineární kombinace bázových matic
dělili)
a spočítáme lineární kombinace bázových matic
![]() s koeficienty z
s koeficienty z
![]() a
a
![]() .
Tím dostaneme aproximace původního obrazu
.
Tím dostaneme aproximace původního obrazu
![]() a
a
![]() . Samozřejmě nesmíme zapomenout přičíst
ke všem hodnotám z obou matic
. Samozřejmě nesmíme zapomenout přičíst
ke všem hodnotám z obou matic
![]() a
a
![]() hodnotu
hodnotu ![]() , abychom dostali zpět hodnoty z rozsahu
, abychom dostali zpět hodnoty z rozsahu
![]() .
Aproximace
.
Aproximace
![]() a
a
![]() vypadají takto:
vypadají takto:
 |
 |
|
|
|
Vidíme, že na obou aproximacích jsou ošklivé artefakty způsobené zejména oním dělením ![]() a následným zaokrouhlováním.
Dále je vidět, že aproximace
a následným zaokrouhlováním.
Dále je vidět, že aproximace
![]() jakoby ztrácí ostrost. To je dáno tím, že jsme jí odtranili souřadnice odpovídající bázovým
maticím s vysokými frekvencemi. Nicméně, když si zobrazíme tyto výsledky v původní velikosti 100x88 pixelů, není to už
tak strašné, jak ukazují následující obrázky:
jakoby ztrácí ostrost. To je dáno tím, že jsme jí odtranili souřadnice odpovídající bázovým
maticím s vysokými frekvencemi. Nicméně, když si zobrazíme tyto výsledky v původní velikosti 100x88 pixelů, není to už
tak strašné, jak ukazují následující obrázky:
 |
 |
 |
| originál |
|
|
Rostislav Horcik 2009-01-04